Arbeitsgruppe Franziska Matthäus – Forschung
Agenten-basierte Modellierung
Wir nutzen agentenbasierte Ansätze um Grundprinzipien koordinierten Verhaltens multizellulärer Systeme zu verstehen. Diese Modellansätze beschreiben jede Zelle als diskretes Objekt und beinhalten mechanische Zell-Zell-Interaktion, (dichteabhängiges) Wachstum und Teilung, aktive Bewegung, sowie Mechanotransduktion. Simulationen mit diesen Modellen basieren auf der numerischen Lösung grosser Systeme gewöhnlicher und stochastischer Differentialgleichungen, oft in Grössenordnungen von 105 - 106 Gleichungen. Die diskreten Objekte (Zellen) können zusätzlich mit einer dynamischen Umgebung interagieren, z.B. durch die Wahrnehmung, Produktion oder Aufnahme chemischer Signalstoffe. Anwendungsbeispiele sind die Dynamik von Modellsystemen wie Organoiden und Späroiden, oder Entwicklungsprozesse (Hautmusterbildung, Embryonalentwicklung von Insekten).

Dichte-basierte Modellierung
Zur Beschreibung von Prozessen in der Hautmusterbildung entwickeln wir derzeit ein mathematisches Modell auf Basis partieller Differentialgleichungen. Das Modell koppelt die raumzeitliche Dynamik der Zelldichte mit der Konzentrationsdynamik interagierende und diffundierender chemischer Substanzen. Hierbei werden zwei verschiedene Musterbildungsprozesse kombiniert: Reaktions-Diffusion-Systeme (Turing-Systeme), und Chemotaxis. Beide Systeme sind sowohl mathematisch auch experimentell gut bekannt, aber erst vor kurzem wurde festgestellt, dass beide Systeme in der Haarfollikel-Entwicklung interagieren. Mit Hilfe mathematischer und numerischer Analyse untersuchen wir in diesem System die Rahmenbedingungen für Musterbildung, sowie die Form und Regularität der entstehenden Muster.

Bildverarbeitung
Wir nutzen verschiedene Bildverarbeitungsmethoden um quantitative Parameter und funktionale Abhängigkeiten in den biologischen Daten zu identifizieren, die dann Eingang in unsere Modelle finden. Wichtige Methoden sind hier die Segmentierung & morphologische Analyse, Einzelzell-Tracking und Particle Image Velocimetry (PIV). PIV ist eine korrelationsbasierte Methode um Bewegungsanalysen für kollektiv migrierende Zellverbände zu erlangen, und liefert auch gute Ergebnisse, wenn Zellmaterial nicht markiert ist und nicht segmentiert werden kann. Kürzlich wurde in unserem AK ein neues Softwarepaket in der Progammiersprache Julia entwickelt, welches PIV Analysen jetzt auch für 3D time-lapse Videos erlaubt. Zudem nutzen wir Segmentierung und Polygon-Approximation von Zellformen um mechanische Parameter in Epithelgeweben zu inferieren.
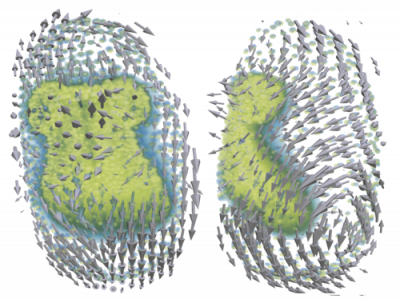
Inferenz mechanischer Eigenschaften
Kraftinferenz is eine computer-gestützte Methode um mechanische Spannungen und Drücke aus statischen Mikroskopiebildern zu bestimmen. Hierfür verwenden wir ein biomechanisches Modell und ein mathematische Inversionsmethode. Um tiefere Einblicke in multiskalen Effekte von Kraftweiterleitung von einzelnen Zellen bis zu ganzen Geweben zu gewinnen und ihre formenden Eigenschaften auf ganze Organismen zu verstehen, ist es von großem Interesse die Raum-Zeit Dynamik der Kräfte zu untersuchen. Als nicht-invasive, observierende Technik benötigt Kraftinferenz keine mechano-sensitive Messsonde, um das Gewebe zu untersuchen und ist in der Lage instantan Ergebnisse für das gesamte Gewebe zu liefern. Wir verwenden Bayes'sche Statistik um die Topologie-bedingte Unterbestimmtheit in einem System aus linearen partiellen Differentialgleichungen zu überwinden. Wir verwenden Kraftinferenzmethoden um die Kraftdynamiken in zeitlichen Daten von Wundheilungsstudien und drei-dimensionalen Daten der Embryogenese von Tribolium castaneum zu untersuchen.



